The wave equation for sound

What are the physical principles that give rise to sound waves? What is the speed of sound? How does the specific acoustic impedance relate pressure to particle velocity? This is a support page to the multimedia chapter Sound. It gives background information and further details.

When we analysed a transverse wave (that in a string), we used y as the displacement for a wave travelling in the x direction. In a longitudinal wave, displacements are parallel to the direction of the wave. When analysing a longitudinal wave, we still use y for the displacement, but remember that this displacement is in the x direction.


The wave we analyse here is sound in an elastic medium, such as air. Let’s consider a one dimensional wave travelling in the x direction. We’ll consider a section with cross section A. (We might picture a wave travelling through a pipe, and neglect the viscous and thermal interactions at the wall.) Here’s what we shall do to analyse sound propagation:
• First, look at how spatial variations in displacement produce compression or expansion and thus derive how the pressure depends on displacement.
• Second, we’ll apply Newton’s second law to see how spatial variations in pressure accelerate the air, and thus change the displacement.

Compression: how displacement affects pressure

We'll consider the motion of an element of our medium, whose position, when there is no sound wave disturbance, is between x1 and x2. We’ll make the distance between x1 and x2 much less than a wavelength of sound, and later shall take the limit of very small distance.

So the undisturbed volume of this element is

V = A(x2 – x1)

and, using the density ρ and cross section A, its mass is

m  =  ρV  =  ρA(x2 − x1)     (1).

At any time t, y is the average displacement of the molecules in the x direction. (I write ‘average’, because of course in a gas, the individual molecules have their own random motion superimposed on the average or bulk motion that we are analysing.) So the illustration shows that, at some time t,
- the medium whose equilibrium position is at x1 is moved to x1 + y1 and
- the medium whose equilibrium position is at x2 is moved to x2 + y2.

The new volume of our element of air is

    V + δV  =  A(x2 + y2 − x1 − y1)   and, using (1), we have

    δV  =  A(y2 − y1).

When a medium is compressed, its pressure rises. The ratio between the pressure increase p and the proportional volume reduction is called the volumetric modulus of elasticity , defined by

So the pressure in our element, when it is displaced as shown in our diagram, is

,     so    

In the limit where x2 – x1 is very small (see Introduction to calculus), this gives us the relation between displacement y and pressure p:

  (2)

Newton’s laws: how pressure variations produce displacements

Now to apply Newton’s second law. The absolute pressure at x1 is PAtm + p1, where PAtm is undisturbed atmospheric pressure. So the pressure on the left, acting on area A, exerts a force to the right of (PAtm + p1)A. Similarly, at x2, the force on the right, acting to the left, is (PAtm + p2)A. So the nett force to the right is

F  =  (p1 − p2)A.

Let’s take the average displacement of our element as y (where y1 < y < y2). So, taking the second derivative with respect to time, its acceleration to the right is

Equation (1) gives the mass and the two equations above give F and a, so  F  =  ma  becomes

We rearrange, reverse the order of p1 and p2 and cancel A to give

In the limit of very small distance x2 – x1, this gives

The wave equation and the speed of sound

Equation (2) gave us so combining this with the equation above we have

(3)

If you remember the wave in a string, you’ll notice that this is the one dimensional wave equation. When we derived it for a string with tension T and linear density μ, we had

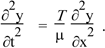
We showed then that this has wave solution with speed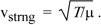  

Let’s do it again here: if we seek a solution

y  =  ym sin (kx − ωt)

and take derivatives, we have

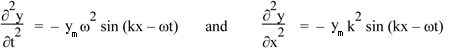
So this is a solution provided that  (ω/k)2  =  /ρ.  Now ω/k   is the wave speed (see travelling_sine_wave for revision) so we have, for the speed of sound:

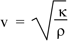
Let's see the analogies: The tension in the string provides a restoring force; so does the elasticity of the medium here. The inertia was provided by the mass per unit length μ of the string, here by the mass per unit volume ρ of the medium.

Although we imagined that our element was air, we have so far only assumed that it is elastic. So this equation is true for longitudinal waves in any elastic medium. For air, we can give a value for the elastic modulus .

In a page about an ideal gas we show that, during adiabatic expansion and compression, the pressure P and volume V are related

PVγ  =  constant,

where γ is the adiabatic constant, or the ratio of the specific heat at constant pressure to the specific heat at constant volume, which is about 1.4 for air. (We notice in passing that this is a nonlinear equation.) Taking natural logs of both side, we have

ln P + γ ln V  =  constant.

Now d(ln x)  =  dx/x   (revise here) so taking derivatives gives us

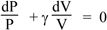
so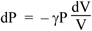      

(Although we remarked above that the P(V) equation is nonlinear, we now see that changes in pressure and volume ΔP and ΔV are proportional if ΔP/P is small. A pascal is already a very loud sound at normal frequencies, and atmospheric pressure is about 100,000 Pa, so sound waves in air are usually linear to an excellent approximation.)

The definition of the bulk modulus (see above), expressed as a differential, is

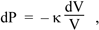
so combining the two equations above we have

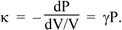
So the speed of sound in an ideal gas is

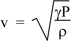
For air at atmospheric pressure (P = 101 kPa) and at T = 20 °C, the density is 1.20 kg.m−3. Taking γ = 1.4 gives a speed of sound of 343 m.s−1.

Specific acoustic impedance

Let’s relate the velocity and pressure, using the solution above:

y  =  ym sin(kx − ωt)

The particle velocity is

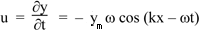
Using equation (2), we have

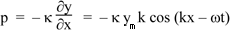
The specific acoustic impedance z of a medium is defined by p/u, so, using the equations above

z  =  κk/ω.

Above, w e had κ/ρ  =  v2, above so κ = ρv2. We also had ω/k = v. Substituting these gives the specific acoustic impedance

z  =  ρv.

Our next step is to relate pressure, flow and power. We do that via the acoustic impedance, which we have just defined as the ratio of the acoustic pressure p to the flow U, where U = uA, where A is the cross-section through which the wave passes. We'll continue on a new support page, on acoustic impedance, power and intensity. See also Compliance, Inertance and Impedance and Acoustic impedance spectrum measurement.
Creative Commons License This work is licensed under a Creative Commons License.