|
|
|
|
牛顿定律：背景和局限性在 Physclips第五章这个多媒体课程中介绍了牛顿定律。本页给出了深一层次的背景。特别指出了牛顿定律的理论基础和局限性。
牛顿定律的不同形式
牛顿第一定律：任何一个物体总是保持静止状态或者匀速直线运动状态，直到有作用在它上面的外力迫使它改变这种状态为止。
牛顿第二定律：物体的速度变化正比于保持所受的外力，速度变化的方向与外力方向相同。
牛顿第三定律：对于每一个作用，总有一个等量反向的反作用：或者说两个物体之间的相互作用总是相等且反向的。
牛顿第一定律和第二定律 的结合： F = ma, 这里如果F = 0就得到第一定律。 正如我们之前提到的，成对出现的力之和为零。比如，我作用在椅子上的力等于椅子作用在我身上的力，或者地球对月球的引力等于月球对地球的引力。或者更一般地说，对于物体1和2，其两者之间的任意相互作用 牛顿第三定律: F1,2 = - F2,1 ， 或者 F1,2 + F2,1 = 0。 对于有限体积的物体，有人也许会问加速度是什么意思。这里，a是其质心的加速度。这点我们会在Physclips上的质心单元中接触到。另外我们也会在动量和能量单元中接触到牛顿定律的更一般的形式。 牛顿定律适用吗？惯性系对比非惯性系
在上述的情况下，如果我们忽略空气阻力，两个观察者都能肯定球的飞行受到了非横向力的作用。在左边的动画中，坐在旋转台上的观察者Zoe看到球在横向加速，这违反了F = ma。相反，坐在地上的观察者Jasper，则看到球非横向加速。但他看到旋转台和扔球者均由于圆周运动而加速。所以Jasper看到的是遵循牛顿定律的情形（非常好的近似），而要解释Zoe的观察结果这是由于Zoe的参考系在加速的缘故。 所以，牛顿定律在哪个参考系中适用呢？这样的参考系被称为惯性系。牛顿定律不适用的参考系（比如Zoe的）被称为非惯性系。除了进行牛顿的实验，有没有什么方法可以判断一个参考系是惯性还是非惯性的呢？ 事实上是有的：就是看着远处的星星。但这会引出相对论的话题，以及伽利略，牛顿，马赫和爱因斯坦的工作。想要了解更多，请见： 牛顿定律可以用于不同的惯性系吗？
这个动画也来源于我们的相对论网站，在这个网站上详细讨论了相对运动。但在这里，为了简洁地推导出重要的结论，让我们把球的运动作为一个实例来看一下。 假设火车以速度v运动，由一个站在火车站的人观测得到。让我们给这个观察者x，y坐标，如图所示。相对这个坐标系（相对火车站静止），设球的位置为r。相对火车坐标系（x'，y'坐标系）)，设球的位置为r'。注意我们用 ' 来表示相对于火车的坐标系中的值（比如x'，y'，r'）。设火车坐标系的原点的位置为p，这是在x，y参考系中的值。 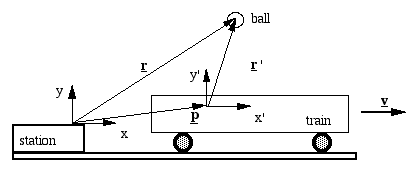 在火车站参考系中，火车在任意点的速度是v。对时间积分，可以得出其位置r为
现在让我们把r和r'以及它们的导数联系起来，记住r'是相对x'，y'参考系而言的。
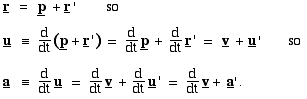 我们假定，相对火车站，火车没有速度变化，所以v对时间的导数为零。这给了我们一个重要的结果
换句话说，两个观察者会得到相同的加速度值。所以，如果火车站是一个惯性系，那么a = F/m，这里m是球的质量而F是作用在球上的合力。 如果两个观察者同意力和质量是一样的，即他们会得到相同的F和m值，而之前我们已经看到两者的加速度值是相同的：a = a'。因此，相对惯性系匀速运动的参考系也是惯性系。 这里我们没有提到之前作的另一个假设，这与对时间求导有关。我们默认了两个参考系中时间是相同的。如果你没有注意到这个假设，没什么关系——在牛顿到爱因斯坦的这段时期里这一点从来就没有被注意过。但是，在学习相对论时这个假设必须考虑，在相对论网站上我们就是这样做的。 F = ma：定义了F吗？定义了m吗？这是物理定律吗？它能表示三条定律吗？
什么是F？力的概念是一个物体与环境之间的机械作用或者反过来环境对物体作用的描述，也因此而被引入讨论的。如果两个较大质量的物体相互非常靠近并且远离其他物体，我们会观察到它们向着对方加速。因此我们可以定义引力并定量描述它。其它的力类似，正如之前看到的，根据定义，施加在物体上的一个（合）力使其加速。那么，如何定量描述呢？ 我们可以通过F = ma来测量力的大小和方向。我们可以通过“力平衡”即让F1 + F2 = 0来比较两个力：合力为零这样（在惯性系中）就不会有加速度产生。例如，当我们用天平称重，通常是调整电磁力让它和所称物体的重力相等且反向。（实际上它们也是杠杆。）这些测量结果明确地告诉了我们那些对于力的理解。从观察结果得到的信息是物体与环境的交互作用。其速度也许变化也许不变。 有时候我们可以感受到力：脚或屁股碰到椅子时就能直接感受到。但大多数情况下，我们无法直接感受或者观察到力。力出现在我们的模型中，即我们的解释中。通常力和直接的观察结果多少是有点区别的。因为力通常是有别于观察结果的，对于它们的描述，理论上说多少是有点任意的。
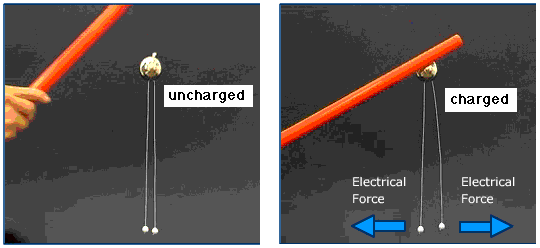 在这张图中(来自电和磁的背景页），我们从电相互作用的角度解释了观察到的现象，但这个解释本身还取决于引力和弦张力的模型。 有时候在模型中把力描述为一定距离上或者通过场来实现的作用（这两个在逻辑上是等价的）。正如我们在能量单元中所展示的，可以用势能的分布来建立模型而不用力。大部分情况下，这些不同的模型在逻辑上几乎是等价的。（但在过去，一些哲学家认为这些图片是不同的：牛顿的图看起来像是原因和效果，而哈密尔顿的能量图看起来更像是目的。） 在很小的尺度上，通过分析虚粒子的交换来研究力。通常在很小的尺度，力这个参数在模型中没什么太大用处，因为在这个尺度上位置，速度和加速度很难定义。更多细节请见测不准原理。 什么是m？
引力质量，mg，在另一方面，可以定义为mg = W/g，这里W是物体的重量而g 是所在位置的引力场。 伽利略的著名实验，下面展示的David Scott的版本，以及之后一些更加复杂和精确的实验表明mg和mi是呈比例的，因此可以通过单位的变换使它们相等。
但是对于为什么亚里士多德是错的而伽利略是正确的，没有理论上的解释：正如科学的各个领域，观察和实验结果就是这样的。理论上看，mg和mi可以是不同的*。两者呈比例这一点并不是巧合而是马赫原理。两者是不可区分的——即等效原理——也是爱因斯坦的广义相对论（爱因斯坦的引力理论）的起点。 * 先锋10号和11号太空探测器现在离太阳的距离比海王星离太阳的距离还远。先锋异常指的是这些深太空探测器航程后期的实际速度变化和考虑了行星引力作用，潮汐效应，光压和其他一些小的效应后的计算结果之间的差别。一些研究人员认为这个差别是计算误差导致的，其他人则认为这可能是未知的物理定律作用的结果。一些人建议用非牛顿力学来解释这个差别。 是的，但m究竟是什么？
许多物理学家猜测有一种还没有发现的场，希格斯场，对于决定一些基本粒子的质量起着作用。在某些情况下，粒子与希格斯场的相互作用决定了粒子的质量。和希格斯场联系在一起的粒子叫希格斯玻色子，只能通过比目前实验达到的能量更高一些的能量来得到。欧洲核子研究组织（CERN）的大型强子对撞机就是用来制造*希格斯玻色子并测量其性质的仪器。当“希格斯子”发现时，我们也许可以更好地认识质量。但是，即使没有希格斯子，我们仍然可以讨论质量的来源。 如果这个理论最终是正确的，那就能解释电子质量以及部分的中子和质子（质量比电子大数千倍）质量的来源。事实上，中子和质子的大部分质量（以及绝大部分常规物体的质量）很可能是由于一个外部效应，比起希格斯场，人们对它有更多的了解。很多物理学家猜测大部分的普通质量只是E/c2。即这只是爱因斯坦著名等式E = mc2的变形。质量和能量是可以相互转化的（通过非常大的转化因数c2），或者对于一些做理论的学者来说，它们是等价的。量子色动力学（QCD） 分析了“普通”的核粒子比如中子和质子是如何由夸克组成的，夸克之间通过胶子的色电力场相互作用。（一个量子色动力学的类比是质子和电子通过光子的电场相互作用的。） 根据QCD，中子，质子和大部分核粒子的几乎所有的质量是由于分布不同的夸克和反夸克的能量，因为量子不确定性，夸克和反夸克无法完全相互抵消色电荷。（更多背景请见E = mc2，牛顿力学和相对论中的能量以及测不准原理）。 到底是怎么回事还不清楚。能量取决于夸克和胶子是如何被限制的，而QCD理论本身无法给出这个限制的尺度——目前，这是根据经验得到的。也许这个尺度也来自希格斯场本身。有些人怀疑这与暗物质有关。这个问题也许很快就会解决。不过，很可能你大部分的质量是存储在中子和质子中的能量，而它们的夸克和胶子处于不同的状态。 当然这并不能告诉我什么是能量。Physclips有一个关于能量的单元，但在那里把能量和力联系起来了，所以如果我说这已经把问题解释清楚了你也许会指责我这是在循环推理，尽管我认为这个单元确实介绍了很多与能量有关的知识。另外，QCD没有解释电子的质量，也不能解释中子和质子质量的所有来源。一些读者也许也在帮忙：如果你在欧洲纳税，那么你就在赞助大型强子对撞机寻找希格斯玻色子。 但是，我们可以把粒子物理放在一边，然后说质量（至少一定程度上，其能量）有一种由牛顿第二定律所定义的形式。所以我认为F = ma确实可以定义质量和力，也是可以检验的定律。如果你对此还是不满意的话，你会注意到在物理中总是有些推理的起点的，就像数学中的一些假设和公理被作为推理的起点一样。 *所以，怎样才能创造希格斯玻色子呢？大型强子对撞机对两束质子加速或者让原子核在27 km长的轨道中反向运动。当速度达到光速的99.99999%时，它们碰撞。 大部分的动能会转换成粒子-反粒子对。有时候，（希望）能产生很难观测到的希格斯子。这是一个非常大的研究项目。比如说对撞机需要用100吨液氦来让磁铁冷却。 如果m变化会怎么样？
如果质量变化会怎么样呢？在这种情况下，我们要用更一般的牛顿第一和第二定律，用动量的定义p = mv。然后我们把牛顿第一和第二定律写成这样：
对于质量不变的情况，这个表达式当然可以化简到熟悉的F = ma。我们会在动量单元中讨论。在很多情况下，第二项是可以忽略的。但请记住有些例子中你可能要用到这个等式。 牛顿第三定律
力总是成对出现，它们的和为零。 在动量单元中，我们介绍了更一般的定律，它包含了牛顿三大定律：就是动量守恒定律：
这个更一般的定律，在我们目前看来是完全正确的。还有一个甚至有点奇怪的理由但能解释为什么它是正确的。：请见牛顿第三定律和人择原理。但正像如果m变化 F = ma 就不适用一样，我们必须指出如果忽略某些效应的话，牛顿第三定律并不适用。 例如，我们考虑两个移动电荷之间的磁相互作用，通常这些力的和不为零。这种情况下，还必须考虑电荷加速引起的相对论效应和辐射动量。
结论
在这些限制之外，我们可以发现，在宏观尺度以及较大的力和能量的范围中，牛顿定律都是适用的并且也是大部分物理和工程的基础。但如果你在要处理非常小的尺度或者高能量时，那你必须得学习一些量子力学和相对论的知识——这也会是一种乐趣的！在力学的最后一章，有一个部分定量描述牛顿力学的局限性。 用保龄球和弹簧来演示牛顿定律下面的视频剪辑中用一个弹簧来加速一个保龄球。正如这些图片所示，可以从弹簧是否拉伸来判断弹簧是否在施加力。用视频剪辑中的单帧按钮来观看。
实例：Circe和圆周运动 |
 |
|
||||||||
F = ma公式确实定义了力和质量。粗看这句话会觉得这是赘述。但是，这个公式的名称本身，即科学定律，理论上是可以证伪的。
在多媒体课程中还记得那个问题吗？那个人对马说“驾”（让马“往前”的意思）。那匹马回答说：“这没有意义。牛顿第三定律指出马车作用在我身上的力等于且和我作用在马车上的力反向。两个力的和为零，所以加速度为零。”你会怎么回答那匹马呢？
