

 |

|
|
|
分贝:什么是分贝? 分贝:dB,dBA,dBC,dBV,dBm和dBi?它们是什么?它们与响度、方和宋的关系如何?本页面将对这些概念进行描述和比较,并给出音频实例。这个页面可以让您测试您的听觉响应,并与标准的听力曲线进行比较。该页是多媒体章节声音和量化声音的背景资料页。
定义和实例分贝(dBis)是用来衡量声级的,但在电子,信号和通信中也有广泛应用。分贝是一个用来描述比率的对数单位。这个比率也许是功率,声压,电压或者强度或者其他。之后我们会把分贝与方和宋(与响度有关的单位)联系起来。但首先,为了对一些对数单位有些概念,让我们看一些数字。(如果忘了,请看什么是对数?)例如,假设有两个扬声器,一个播放的声音的功率为P1,另一个播放相同的声音但更响一些,功率为P2,其他条件(播放距离,频率)都保持相同。 两者分贝上的差异被定义为 10 log (P2/P1) dB 这里log以10为底。 如果后者的功率是前者的2倍,则分贝上的差异为10 log (P2/P1) = 10 log 2 = 3 dB. 如10 log (P2/P1) against P2/P1关系的图中所示。继续这个实例,如果后者的功率是前者的十倍,则分贝上的差异为10 log (P2/P1) = 10 log 10 = 10 dB. 如果后者的功率是前者的一百万倍,则分贝上的差异为10 log (P2/P1) = 10 log 1,000,000 = 60 dB. 这个实例显示了分贝量度的一个特征,这在讨论声音时很有用:可以用不大的数字来描述非常大的比率。但要注意分贝描述的是一个比率:至此我们还没有提及过扬声器的辐射功率,只是功率的比率。(也请注意定义中因子10使得decibel这个词中带有 'deci')。
|
20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB 这里log仍以10为底。
我们若把功率减小一倍会怎样?log2为0.3,故log1/2为-0.3。所以若把功率减小一倍,功率减小同时声级减小3 dB。再把功率减小一倍(减小到原来的1/4)声级再次减小3 dB。如果功率持续减半则会有这些比率。
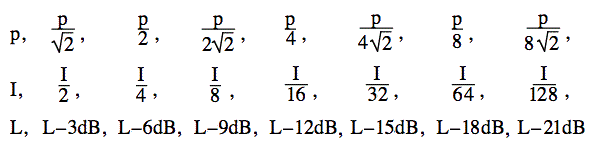
如果将两个相同的声音叠加在一起会怎样?声强会增加1倍吗(增加3 dB)?或者声压会增加1倍吗(增加6 dB)?这是一个常见的问题,答案并不直观,请见常见问题解答。
以上我们看到,声功率减小1倍,声压则减小2的平方根倍,声级减小3 dB。 这也是我们在第一段中讨论并将在以下音频文件中展示的。
|
|
第一个声例是白噪声(所有可听见频率的混合,正如白光是所有可见光的混合)。第二个声例是同样的噪声,但电压减小了2的平方根倍。2的平方根的倒数大约是0.7,因此-3 dB对应电压或者声压原始值的70%。绿线表示电压随时间的变化。红线表示随时间的指数递减。请注意每两个声例电压减小50%。 另请注意,电压增大一倍,响度并不会有太大的变化。之后我们会深入讨论。不过,在选择重放设备时记住这点非常有用。音频文件和flahs动画由John Tann和George Hatsidimitris制作。 如果动画无法播放,或者需要.wav文件,请见无flash版 |
|
|
1分贝非常接近声级的最小可觉差 (JND)。当你试听这些文件时,你会注意到最后一个声例比第一个轻一些,但后一个声例比前一个轻就不是很明显了。10*log10(1.26) = 1,因此声级增大1 dB,功率必须增大26%,或者电压增大12%。 |
|
|
你也许会注意到结尾比开始轻一些,但很难注意到相邻声例之间的差别。10*log10(1.07) = 0.3,因此声级增大0.3 dB,功率必须增大7%,或者电压增大3.5%。 |
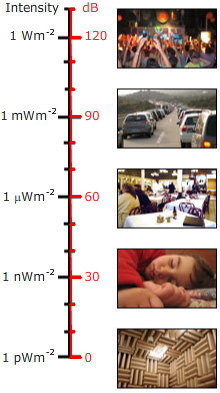 之前我们提到分贝是一个比率概念。因此,要表示一个声音的声级而不是一个比率则必须选择一个参考级。对于声压级,参考级(空气)通常是20微帕斯卡(20 μPa),或者0.02 mPa。(这个值非常小:一个大气压的百亿分之二。不过,这也是人耳听觉在最敏感的频率范围内的灵敏度极限了。通常只有年轻人或者没有暴露于嘈杂的音乐或其他噪声的人才具有这种灵敏度。具有入耳式扬声器的音乐播放设备("walkmans")能够在耳中产生很高的声级,在发达国家被认为是造成年轻人听力受损的重要原因。)
之前我们提到分贝是一个比率概念。因此,要表示一个声音的声级而不是一个比率则必须选择一个参考级。对于声压级,参考级(空气)通常是20微帕斯卡(20 μPa),或者0.02 mPa。(这个值非常小:一个大气压的百亿分之二。不过,这也是人耳听觉在最敏感的频率范围内的灵敏度极限了。通常只有年轻人或者没有暴露于嘈杂的音乐或其他噪声的人才具有这种灵敏度。具有入耳式扬声器的音乐播放设备("walkmans")能够在耳中产生很高的声级,在发达国家被认为是造成年轻人听力受损的重要原因。)
如果声级是86 dB,意味着
20 log (p2/p1) = 86 dB
这里p1是声压的参考级,p2是待知的声压。两边同时除以20:log (p2/p1) = 4.3
p2/p1 = 104.3
4是10000的对数,0.3是2的对数,因此这个声音的声压是参考级的2万倍(p2/p1 = 20,000)。86 dB的声音很响,但还不危险,如果不是持续很长时间的话。0 dB是什么意思?这个声级在测得的强度等于参考级时出现, 即声级对应于0.02 mP。因而有
声级 = 20 log (p测量值/p参考值) = 20 log 1 = 0 dB
请记住分贝是比率值。0 dB在计算比率为1的对数时出现。因此0 dB并不意味着没有声音,而是一个声压等同于参考声级的声级。这个声压很小,但不是0。负声级也是可能的:- 20 dB意味着声压比参考声压小10倍,即2 μPa。并不是所有的声压都是等响的。这是因为人耳对所有频率的响应是不同的:我们对频率在1 kHz到4 kHz(每秒1000到4000次的振动)的声音更敏感。鉴于此,声级计通常带有一个滤波器,其对频率的响应同人耳相似。(关于这些滤波器的更多请见下文介绍。)如果使用了“A计权滤波器”,声压级单位就是dB(A)或者dBA。A计权的声压级非常容易测量,因而使用广泛。但它仍然不同于响度,因为这个滤波器和人耳的响应还是有差异的。想要了解响度,则需要查阅一些人耳对频率的响应曲线,如下。(或者您可以测试您的听觉响应。)
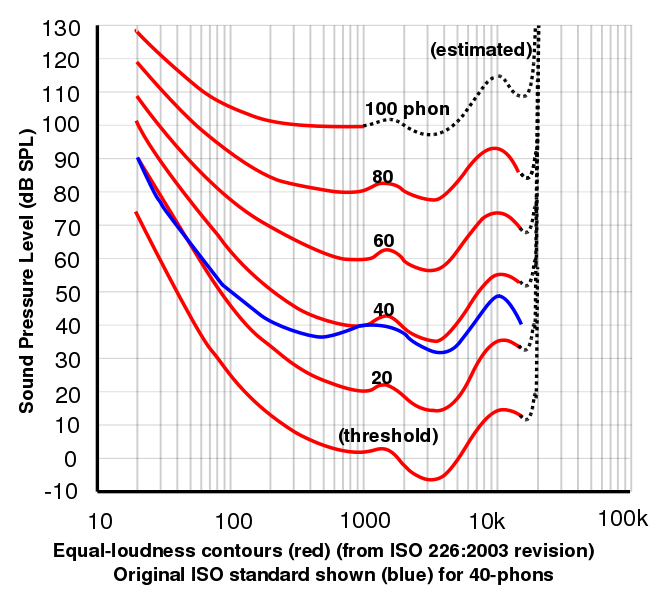
这张图, 承蒙Lindosland的允许,为2003年来自世界标准组织实验所得的等响曲线数据。频率相关的等响曲线通常也被称作Fletcher-Munson曲线,来源于Fletcher, H. and Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59.
宋来源于心理物理学实验,需要实验对象调节音量直到他们认为音量达到2倍。这一点可以让感知响度与方联系起来。1宋被定义为等同于40方。实验结果来看声级增大10 dB大致对应于感知响度增大1倍。因此这个近似被用来定义方:0.5 宋 = 30 方,1 宋 = 40 方,2 宋 = 50 方,4 宋 = 60 方等等。
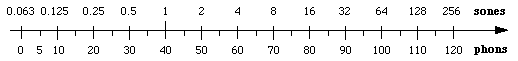
如果能将分贝(仪器可测量的)转换成宋(接近人们感知的响度)岂不是很好?通常你可以在声学手册上找到这样的转换表。但如果你不是很介意精度,你可以说A计权曲线在低至中等的声级范围内接近人耳的频率响应,因此dBA非常粗略得等同于方。然后再使用上述宋和方之间的对数关系转换即可。
绝对电平级 = 20 log (V/V参考值)
简单地,选择1伏特有效值作为电平级,这里电平级写作dBV。这点对于现代模拟-数字转换卡也很简便,因为通常这类设备的最大测量值大约是1伏特有效值。因此请记得保证电平级为负值(小于1伏特)以避免信号峰值被限幅,但这个负值也不能过小(这样信号仍然能比背景噪声大)。
有时候你会见到dBm。这个值过去用来指相对于1毫瓦的电功率分贝,现在有时候仍被这样使用。但是,由于一些历史原因而有些复杂。二十世纪中叶,许多音频线的名义阻抗是600 Ω。如果阻抗是纯电阻,设 V2/600 Ω = 1 mW,则 V = 0.775 V。因此,如果你使用600 Ω负载,1 mW的功率就是0 dBm,也就是0.775 V,电平计也是这样校准的。不过通过这种方法校准后的电平计会有一些问题,即在没有连接600 Ω的负载时也会在0.775 V时显示0 dBm。因此,也许不是很合理地,有时候dBm是指相对0.775 V时的分贝。(我小时候计算器非常昂贵,所以我用我父亲的计算尺,其游标窗口标有0.775以简化这类计算。)
如何将dBV或者dBm转换成dB声级?没有简便的方法。取决于如何将电功率转换成声功率。即使电信号直接输入扬声器,转换也要取决于扬声器的效率和阻抗。当然也许还有功率放大器,以及混音台上测量dBV的位置与你在声场中位置的变化会使情况更复杂。
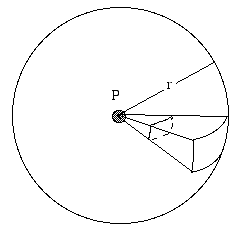
一个声源向各方向等强度辐射的现象称为对称。现考虑一个远离任何反射表面的孤立声源--(比如)鸟在空中鸣叫。以声源为中心,球半径为r。这个源连续输出的总功率是是P。声能量向外辐射并通过球面。如果这个源是对称的,则根据定义,声强I在这个球面上任意处都是相等的。声强的定义为单位面积的功率。球表面积为4 πr2,因此根据定义,通过球面单位平方米的功率(在我们的例子中就是声功率)为:
请注意,很多源都不是对称的,特别是当波长的尺寸小于源的尺寸或者两者接近时。而且,反射通常非常重要,特别是靠近地面或者在室内时。
|
功率变化了10倍,正如我们之前所说的,即10分贝。这里其他条件相同意味着频率响应相同且使用相同的输入信号等。因此频率关系应该是相同的。10分贝对应10方。为了在感觉上获得原响度的2倍,需要增加10方。因此假设扬声器在线性范围内且没有失真或者损坏的情况下,100 W 功率放大器驱动的扬声器(线性范围)的响度是10 W功率放大器驱动的扬声器响度的2倍。(100 W 功率放大器获得的响度是10 W功率放大器的2倍方。)
首先,注意反射可忽略非常重要。在室内这个计算方法不适用。来自墙面(整体产生回声)的反射使计算变得非常不同。在开放的室外,声强与1/r2呈正比,r是离声源的距离。(比例常数取决于地面的反射能力,这里不用考虑,因为在这里的计算中被消去了。)因此,如果我们把距离从R增大到nR,声强从I减小到I/n 2。
根据之前的定义,强度为I 2和I 1的两个信号在分贝上的差别为
例如,若n为2(即2倍远的地方),声强减小4倍而声级从L减小至(L − 6dB)。
根据之前的定义,两个功率为P2和P1信号在分贝上的差别为
电压,就像压力,在功率或强度的表达式中以平方呈现。(电阻R上损耗的功率为V2/R。)因此,根据惯例,我们定义:
(在上述的声学实例中,我们看到以分贝表示的压力比,与功率比相同:这是对压力定义分贝时有一个因子20的原因。值得注意的是,在电压增益的实例中,功率放大器的功率增益未必等于根据惯例定义的电压增益。对于给定的电阻,功率与电压的平方呈正比。但是,功率放大器的输入和输出阻抗通常非常不同。例如,缓冲放大器或者射极输出放大器的电压增益大约是1,但电流增益很大。)
对于工作中的噪声暴露问题,不同国家和省份显然具有不同的法律以及不同的执行力度。对于8小时轮班工作,许多规定要求连续噪声的上限是85 dBA。噪声每增加3 dB,暴露在噪声下的允许时间减半。因此,如果在你工作的夜总会,你耳边的音乐若达到了100 dBA,则暴露在这种声音下的允许时间为15分钟。对于如枪支以及爆破设备产生的瞬时噪音也有上限。(例如白天任何时间峰值不得超过140 dB。)有许多文件提供了如何避免暴露于噪声的建议,针对噪声源(即降低音乐的声级),声源与耳朵之间(即音乐会上把扬声器放在远处) 以及耳朵(即戴耳塞或者工业级听力保护装置)。工作中的噪声管理与听力保护是澳大利亚新南威尔士州(作者所在地)的执行条例。
|
|
|
|
What is a logarithm? A brief introduction.
| |||||||||||
| |||||||||||