Negative thermal expansion and entropic forces
Why does a rubber band contract on heating? Heat steel and it expands. Heat a rubber band and it contracts – as our rubber band heat engine demonstrates: sketch at right. Many other polymers also contract with increasing temperature. Why so? Here we answer this in molecular terms. Our somewhat simplified answer also leads us to some interesting ideas, including the role of entropy in forces.
|
|
But first, we could also ask why is it so much easier to stretch a rubber band than to stretch a similarly shaped piece of steel? A large part of the answer here is that, when we stretch steel or most solids, we increase slightly the average distance between atoms, for reasons we discuss on the page on Hookes' law, elasticity, Young's modulus and thermal expansion.
However, when we stretch polymers, very often we are straightening molecules: in terms of the (highly simplified) diagram below, if we go from states represented by the right hand side diagrams to the one on the left, we straighten the molecules and increase their length from L to L0.
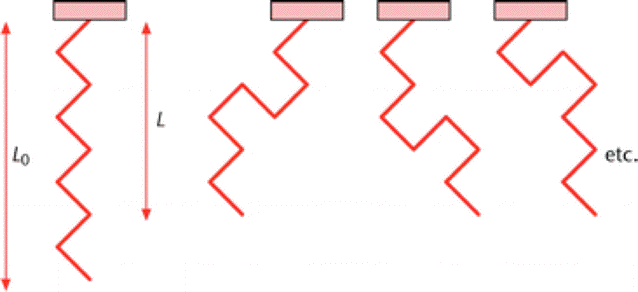
Very often, the lowest energy state of a polymer molecule is the straight (all trans) one, like that shown at left.
So that raises an interesting question: why aren't all the molecules in the low energy state? And, once again, we'll answer this question by considering another question. For the molecules in the atmosphere, the state with lowest gravitational potential energy is zero altitude. Why aren't all the molecules resting on the ground? Practically, this is a very important question: if all the molecules in the atmosphere came to rest on the ground, they would make a layer roughly 10 m thick and most of us – those who live at higher altitudes – would asphyxiate.
The answer is here is that the air molecules have finite temperature and that, because of this, they are distributed in states having different energies, they have highest concentration at ground level, but lower and lower concentrations at successively higher altitudes. It is possible to calculate this distribution using the gas laws (and relatively easy if one pretends that the temperature is constant). But let's try to give a simplified molecular explanation.
The molecular explanation for the distribution of air molecules involves the concept of entropy. At the molecular level, entropy is related to disorder. Physical systems often exhibit a compromise between low energy and high entropy. (Strictly, they often minimise U − TS, where U is energy, T is temperature and S is entropy.) At one extreme: oxygen and nitrogen crystals at ground level would have low energy, but high order; at the other extreme, Earth's atmosphere uniformly distributed over all space would have very high disorder, but also high potential energy. In practice, our atmosphere is a compromise. Further, if we heat the atmosphere, it expands: more molecules are distributed at high altitudes.
So, back to our polymers. The kinked states are less ordered: for any given length L there are more than one such state. The straight state is ordered: there is only one of them. So, at finite temperature, the polymers are kinked. If we raise the temperature, there are on average more kinks (more disorder), and the polymer is shorter.
I hope that many readers will want to know more. I've written a chapter giving a molecular introduction to thermal physics for biologists: the figure above comes from there. In it I explain entropy and the energy distribution, and also the contraction of polymers. The chapter is here.
|
|



