
 |
|
|
Gravity in context in physics
The attractive force that holds the nucleus together -- aptly called the strong force -- is stronger than the electric force over short range: if the nucleus is small enough, the strong force 'wins' and the nucleus is stable. (However, large nuclei are unstable: they divide by radioactive decay: elements with atomic number above about 90 are usually radioactive because the electrical repulsion among 90 protons tends to defeat the attraction of the strong force.) This appendix has a chart showing the known forces and some relations among them. So why does gravity rule the universe? Forces, acceleration and Newton's laws of motion
Galileo and Newton: forces and accelerations. (These sections also have multimedia tutorials on the home page of Physclips.) Before Galileo and Newton, Aristotle's writings dominated European thought about physics. Oversimplifying a little, it was thought that:
Demonstrations of forces and acclerations
See more of these film clips below. Newton's law of gravity
In 1687, Isaac Newton wrote "I deduced that the forces which keep the planets in their orbs must be reciprocally as the squares of their distances from the centres about which they revolve; and thereby compared the force requisite to keep the Moon in her orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly." Here, \translated into modern units, is Newton's calculation of the centripital acceleration of the moon due to its circular orbit around the earth. Its direction is towards the earth. We can work out its magnitude from our equation ac = 4π2r/T2, using the distance from the earth to the moon (380,000 km) and its period of 27.3 days. 
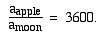
 so so
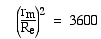
In modern notation, we write Newton's law thus: if two bodies with masses m1 and m2 are separated by a distance r, then the attraction between them is 
Why is gravity inverse square? is an interesting question, and one explanation is geometrical. If we picture field lines radiating uniformly from a symmetrical mass distribution, the intensity of the field (the number of field lines per unit area) is the total number of field lines (say N) divided by the area of a sphere, which is 4πr2. So the field strength is N/4πr2. This description is rarely used for gravity. In electricity, however, the analogous relation between geometry and the strength of the field is standard and is called Gauss' Law. Magnetism is also an inverse square law, and one of Maxwell's equations is usually called Gauss' law for magnetism. If we were to use the same mathematical formulation for gravity as for electricity and magnetism, we should also have a factor 4π in the denominator. However, for gravity, the factor (1/4π) is absorbed in the constant G. So the 1/r2 factor that it comes from the fact that we live in a universe with three dimensional*, approximately flat spatial geometry. In a flat space, the interior angles of triangles add to 180°, the area of a sphere is 4πr2 and electromagnetic and gravitational force are proportional to 1/r2. If the angles of a triangle added to less than 180°, then these forces would decrease more strongly with r and conversely. * This argument applies only to dimensions that are large enough to be measured. Gauss' law does not rule out the existence of further dimensions, provided that the entire size of the universe in these dimensions is smaller than the smallest size we can measure. This is the escape clause available to supporters of m theory and string theory. One could argue that some nuclear physics experiments measure on the fm scale, so that the size of the universe in any putative higher dimensions must be rather smaller than this.
Inertial mass, gravitational mass and Mach's principle Why does gravity seem to depend on the (inertial) mass? This is another interesting and profound question: the same quantity, mass, that appears in Newton's equations of motion, also appears in Newton's (or Einstein's) law of gravitation. This is not due to a lack of imagination on Newton's part: he thought carefully about this coincidence. Because the two are conceptually distinct, let's separate them. The inertial mass mi is the constant of a body that appears in Newton's combined first and second law, F = mia. It is the constant that quantifies the body's reluctance to be accelerated. The gravitational mass mg is the constant of a body that appears in Newton's law of gravitation, F = − GmgMg/r2. It quantifies the body's interaction with the gravitational field. Why are they the same? Experimentally, they are the same: Newton and many others since have conducted experiments. Or rather, they are proportional, because we could consider G to include any fixed ratio mi/mg. What sort of experiment? Here's an example: take a pendulum consisting of a light hollow container suspended on a light string. We then fill the container with the substance to be tested. In the analysis of the pendulum, the restoring force is proportional to mg. The acceleration is inversely proportional to mi. If the two are proportional, then we find that the period of the pendulum does not depend on the mass. So, we can conduct a series of tests on different substances to see whether the period varies. For instance, if we used water or octane, we should have a relatively high ratio of protons to neutrons. If we use a heavy metal, a low ratio of protons to neutrons. So we can test whether mg/mi varies between protons and neutrons. Another sort of experiment would be to compare the accelerations of objects in one or more gravitational fields. We give examples in this link. One reponse is that this it is not a coincidence, and that the interactions among masses give rise to inertia. This is called Mach's Principle. Another approach is to propose that mi and mg are not merely proportional, but really are the same thing. This is a starting point for Einstein's theory of General Theory of Relativity. The proportionality of mi and mg has been and is still being tested in a number of several very sensitive experiments. We discuss it in the section on gravitation in this link. Newton's shell theorem
Cavendish measures the mass of the earth
Cavendish used his measurements to determine the mass of the earth, Me. An object of mass m at the earth's surface is Re from the earth's centre. The magnitude of its weight is approximately* mg, where g is the acceleration it has in free fall.
Cavendish's value for the mass of the earth was close to the currently accepted value of 5.97 x 1024 kg. Knowing the mass of the earth and its orbit around the sun, one knows the centripital force exerted by the sun on the earth, and so one can calculate the mass of the sun. (The orbits of moons around most of the planets gives the masses of the planets.)
Gravity is a puny forceAlthough measurements of the constant of gravitation are now much more accurate than those made by Cavendish, G is still the least well known of the fundamental constants, simply because gravity is so weak. Let's illustrate this with some values.However, as we mentioned above, the cancellation of positive and negative electrical charge and the limited range of nuclear forces means that, on the large scale, gravity wins. Which brings us to Planetary motion
As long ago as the fifth century BC, Leucippus and Democritus proposed a heliocentric universe, i.e. one in which the planets orbit the sun. On the mistaken assumption that the earth's motion ought to be noticeable, Hipparchus (second century BC) and Ptolemy (second century AD) proposed a universe in which the sun and planets executed complicated motions around the earth.
The Danish astronomers Tycho and Sophia Brahe (1546-1601, 1559-1643) made very many, very careful, naked eye observations of the positions of the planets. He was joined by Johannes Kepler, a tireless calculator. After a long time trying to fit circular orbits and even musical harmonies to the data, Kepler eventually discovered that the data were all well fitted by the following empirical laws. Kepler's laws
Why is it so? What underlying reasons are there for Kepler's laws? It is difficult for a modern person to have a feeling for the magnitude of this puzzle – hence this appendix. For two millenia, this was the riddle of riddles. So Newton's demonstration that the three laws follow simply from his laws of mechanics was a major triumph and secured his fame. Proving the first law requires a reasonable amount of geometry, so we omit it here. In the multimedia tutorial on Physclips we derive the other two. To revise briefly here: For circular motion, with the sun at the centre (see below), the centripital acceleration is, as before
T2 = (4π2/MG)r3 (K2) For circular orbits at least, we have derived Kepler's third law in a few simple equations. The same force that makes the apple fall rules the heavens. The second law, which is animated below, follows just as simply from conservation of angular momentum. The proof, which is given in the multimedia section is repeated here:
Planets of other stars
Satellite orbitsIn the multimedia section, we use the equation derived above, T2 = (4π2/MG)r3, to derive the period of orbits for earth's satellites, using G = 6.67 x 10-11 Nm2kg-2 and Me = 5.97 x 1024 kg. Many satellites, including the international space station, are in low earth orbit, meaning an orbit with a radius a little greater than that of the earth: say 6,500 km. Substitution in (K2) gives a period of about 90 minutes. (So, in Shakespeare's A Midsummer Night's Dream, Puck seems to be out by a factor of two.) Newton gave this nice idea to help explain orbits. First, consider a projectile (Newton imagined a cannonball) fired horizontally from the top of a mountain, over a distance small enough that the earth's surface can be considered flat. No matter what its horizontal speed, its vertical acceleration is g downwards. If we fire it very fast, however, we can no longer neglect the curvature of the earth. At a particular value of the horizontal velocity (about 28,000 k.p.h.), the curvature of the path of the cannonball will match the curvature of the surface of the earth. The cannonball still accelerates downwards at g, but g is now the centripital acceleration of its circular motion, as shown below.
Satellite orbits and "weightlessness"The subject of satellites and the International Space Station raises the topic of free fall and a phenomenon that is ufortunately called "weightlessness". Physicists usually put the word in quotation marks because, in an orbiting spacecraft, an astronaut's weight (his gravitational attraction towads earth) is virtually normal. Indeed, since the moon flights stopped, no human has been far enough from the Earth for his/her weight to be substantially reduced. This may seem puzzling, so let's look more closely. Even on earth, we do not directly sense our weight, because it is applied homogeneously over the whole body. However, if you are seated, you can feel your chair pushing upwards on you with a force of several hundred newtons. The upwards force from the chair and your equal in magnitude your weight (a downwards force). You can also feel your abdominal muscles holding your internal organs in place. These and some other forces give you the sensation of having weight. If the forces from the chair and on your abdominal wall were reduced or zero, you would feel "weightless" – an exaggerated version of the feeling you get when a lift starts to accelerate rapidly downwards, or when you go quickly over a peak on a roller coaster. The three diagrams below show situations that produce free fall. In an orbiting spacecraft, the spacecraft and the astronaut are both accelerating towards the centre of the earth at the same rate. (Their centripetal acceleration is ac = rω2 = v2/r, where ω is the angular velocity, v is the orbital speed and r the radius. In low earth orbit, ac ≅ g.) Their weight – the gravitational force exerted on them by the earth – is what keeps them in orbit: W = mac. However, because they are both accelerating towards the centre of the earth at the same rate, there is on average no force between the astronaut and the spacecraft. This absence of forces from seat, floor, abdominal wall etc is what is commonly but misleadingly called "weightlessness": the astronauts in the space station are not without weight, in fact they have (almost) their usual weight. It's just that they don't feel the force of chairs and floors supporting them, and they don't feel their abdomens holding in their organs.
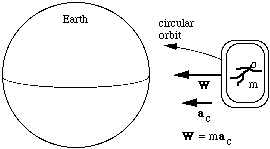 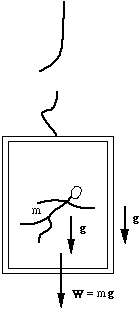 
In figure at right, a NASA airplane (nicknamed the 'vomit comet') cuts the power in its engines and, for about 25 seconds, travels in a trajectory that is nearly parabolic (none of the diagrams to scale, of course). Both the plane and its occupants accelerate towards the Earth at g: all are in free fall. Astronauts are thus exposed to free fall and obtain brief periods of experience in working in the condition of free fall and feeling "weightless". There are some similiarities between the passenger (mass m) in the lift (let's put it at the equator) and an astronaut (mass m) in low Earth orbit. The weight of each is about mg. Both accelerate towards the centre of the Earth at approximately g. The difference is that the spacecraft makes a circle around the Earth in about 90 minutes, whereas the lift makes a circle around the Earth in about 24 hours. The acceleration g is just enough to keep an object in low Earth orbit with a period of roughly 90 minutes. This acceleration is far too great for the 'orbit' of the hapless passenger in the lift. If a satellite loses speed, it gradually spirals in towards the Earth. The horizontal speed of the passenger in the lift is so low that his 'spiral' towards the centre of the Earth is almost a straight line. (There have been a few 'approximately's and 'almost's in the above. If you are interested in the analysis of motion in the rotating frame of the Earth, have a look at the formal analysis of the motion of a pendulum at the Earth's surface.) (What would it feel like if you really were weightless? Suppose you were in a spacecraft far from the sun, other stars, even other galaxies. Then you would be (nearly) weightless. How would it feel? If your spacecraft were not accelerating, then you would feel "weightless", just like someone in the space station. If you fired the engines of the spacecraft, however, you would feel as though you had weight. You could also produce the feeling of weight by spinning the space craft.) (A further approximation: the gravitational force exerted on you by the earth is almost, but not quite, mg. For details, see Why g is not parallel to Fg.)
Orbits and the centre of mass

Using subscripts m and e for the moon and earth, we can write Magnitude of force on the moon due to earth: Fg = mmam = mmω2rm and
The distance between the centres of the earth and the moon gives a second equation:
Solving these gives rm = 3.80 x 108 m and re = 4.7 x 106 m So the centre of both orbits, which is also the centre of mass, is 4700 km from the centre of the earth: it lies inside the earth. (In contrast, the analogous calculation shows that the centre of mass of the sun-Jupiter system lies outside of the sun.) A puzzleAn interesting paradox: why doesn't the moon fall into the sun? Calculate the point on a line between earth and sun at which the gravitational forces exerted on a mass m by the earth (Fe) and the sun (Fs) are equal and opposite. 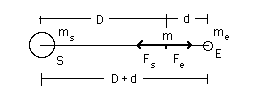
Doing the calculation, we find that the point of equal attraction lies 260,000 km from the earth. But the moon is 380,000 km from the earth! At new moon, the point of equal attraction lies nearly on a line between the earth and the sun (during a solar eclipse, it lies exactly on this line). So, at new moon, will the moon fall into the sun? The problem and the calculation are described here. But I'm not giving answers: it's for you to solve! Gravitational potential energy
The gravitational potential energy U of two objects, masses M and m, at separation r, is obtained from the definition of potential energy, −Ug = ∫ Fg.ds. (Revise potential energy.) Because gravity acts in the direction of −r, we can write Fg.ds as −Fgdr. Substituting from Newton's equation for Fg and integrating: 
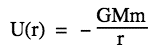
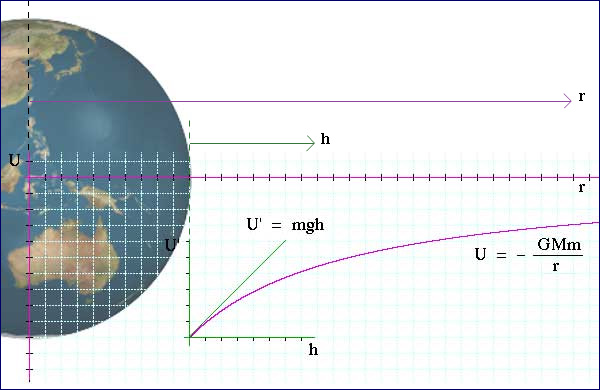
The graph above shows two different expressions for gravitational potential energy of a mass m near the earth. For r > re, we use U = −GMem/r. Very close to the earth (in other words when (r − re) << re), we can use the approximation GMe/re ≅ g and the binomial expansion to write:
Escape "velocity" and black holesThe quotation "What goes up must come down down" is sometimes attributed to Newton. In fact, it was he who proved quantitatively that what goes up need not come down. Let's see why. The following animation uses the graph of potential energy U(r) to show the path of a projectile launched vertially upwards. The kinetic energy K is shown in red, the potential energy U in purple (both histogram and graph) and the total mechanical energy E = U + K is shown in white. Here, E < 0 so, when K goes to zero, U is still negative. Escape "velocity" is minimum speed ve required to escape, i.e. to get to a very large ('infinite') distance from a planet. An object launched from earth with the earth's escape velocity would never return. To achieve this, we need to give it an initial kinetic energy Ki = ½mvesc2 that is at least as great as the magnitude of U near the earth. Rearranging yields 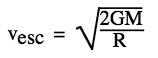
Black holes
Setting vesc = c and rearranging the equation above gives
the 'event horizon' of the black hole. If M lies inside Rblack, then no light escapes outside. Having c2 in the denominator means that this radius is small. For an object with the mass of the earth, it is = 9 mm. The earth is not going to contract to this size, so it won't become a black hole. For the sun, the value is 3 km. The sun is currently made of plasma, so one might ask whether, when it cools and shrinks, it could become a black hole. After all, it is electrically neutral, which reduces the possible repulsion due to electric forces, and nuclear forces, though strong, have a small, finite range. The answer is no: for the sun, the repulsive forces among the atoms are strong enough to prevent gravity from turning it into a black hole. For stars somewhat bigger than the sun, however, these forces are not large enough, and only repulsive nuclear forces are strong enough to resist gravity. Such stars become neutron stars -- like a giant nucleus, in which gravity, intensified by having a huge mass within a diameter of several km, is the main attractive force. Finally, for yet larger stars, even nuclear forces do not provide strong enough force to resist gravity. The result is a black hole, from which light cannot escape. Although it is black -- emitting no light -- radiation can be produced near the black hole. However, this is not how we can find them. The only way we can find them is from the effect of their gravitational field on other stars (as shown in the multimedia tutorial on Physclips) or on light (the effect is like that shown at right). Black hole fusion and gravitational radiation. The big science news of 2016 was the detection by the LIGO collaboration of gravity waves from the fusion of two orbiting black holes. On another page, we do a simple Newtonian calculation of this event and obtain radiation intensity that is of the same order as that calculated from general relativity. (A colleague and I wrote a little essay about this for Nature Physics.) The limits to Newtonian gravity
To be accepted, any new theory of gravity must give virtually the same answer as Newton's in all of the many cases where Newton's theory works, but must also give the right answer for the cases where we know that Newton's theory fails, such as the slight deflection of starlight passing very close to the sun (observable during a solar eclipse) and certain aspects of the orbit of Mercury that cannot be accounted for by considering the effects of the other planets. Several other theories do this, of which one of the simplest and by far the most widely used is Einstein's General Theory of Relativity. Philosophically, General Relativity is very different from Newtonian gravity, in that it doesn't use forces. Rather, the effect of large masses is to curve space, and the curvature of space determines the motion of objects. It is often summarised thus: "matter tells space how to curve, and space tells matter how to move". So, if there are several competing theories that all do better than Newton's, what theory of gravitation should we use? The mission of Gravity Probe B was to conduct experiments to distinguish among some current theories of gravitation, but it had limited results. However, both Einstein's and Newton's theories of gravity have a problem when they encounter quantum mechanics, and that problem involves the very nature of space and time. We explain this further on Gravity, relativity and quantum mechanics. Fortunately, the scale of the problem is that of the Planck length, which is 1.6 x 10-35 metres. This is immeasurably small, and it is perhaps not too surprising that our ideas about space would need to be revised on this scale.
The limits to Newtonian physics
Why g is not parallel to Fg
The diagram above may seem odd, because the vertical of the string is not at right angles to the horizontal. That's because, in that diagram, we exaggerated the angles of the forces, but didn't consider the effects of rotation on the shape of the earth. So, let's hang the mass on a string and leave it at rest, with respect to the earth. As shown, the tension in the string will be almost the same as mg, but not quite. The string hangs vertically, by definition of vertical. However, this direction is not quite parallel to Fg and it does not point exactly at the centre of the earth. A similar argument determines the shape of the earth. The surface of a bowl of water is horizontal, by definition. Here, the normal force and the gravitational force acting on a mass at the surface of the water must also add to give acentrip,, otherwise the water would flow out of the bowl. So the surface of the water – horizontal – is at right angles to the string in our example. The earth's shape is determined by the the forces on it and, on a large scale, it is very close to that of a drop of spinning fluid so, the earth's (large scale average) surface is also, roughly, at right angles to the string. In the animation below, the rate of rotation is exaggerated so that the difference in angle and the tiny eccentricity of the earth's shape – both very tiny in practice – can be seen. What happens if you spin so fast that the string points away from the axis of the earth? The next animation shows this unhappy (but unlikely) result. Appendix: Relations among the forces of nature What IS magnetism? is a derivation showing that magnetism may be considered as an aspect of the electrical interaction.
What IS magnetism? is a derivation showing that magnetism may be considered as an aspect of the electrical interaction.
Appendix: Film clips illustrating Newton's second lawThe film clips below use a spring to accelerate a bowling ball. You can tell whether the spring applies a force from whether it is stretched or not, as in these photos. Use the step frame button on the film clips.
Appendix: Centripetal accleration
See also the section on circular motion, in which this derivation is animated. Appendix: Faust and the music of the spheresSpace travel has made us blasé about motion in the skies. This may give us some flavour of the Mediaeval view: Christopher Marlowe (a contemporary and rival of Shakespeare) created Doctor Faustus (perhaps based on the historical character Paracelsus) -- a philosopher/scientist who sells his soul for knowledge. Here is an extract from the play, in Act VI:
Come, Mephistophiles, let us dispute again, And argue of divine astrology. Tell me, are there many heavens above the moon? Are all celestial bodies but one globe, As is the substance of this centric earth? Mephistopheles: As are the elements, such are the spheres Mutually folded in each other's orb, And, Faustus, All jointly move upon one axletree Whose terminine is termed the world's wide pole; Nor are the names of Saturn, Mars, or Jupiter Feign'd but are erring stars. Faustus: But tell me, have they all one motion, both situ et tempore? Mephistopheles: All jointly move from East to West in twenty-four hours upon the poles of the world; but differ in their motion upon the poles of the zodiac. Faustus: Tush! These slender trifles Wagner can decide; Hath Mephistophiles no greater skill? Who knows not the double motion of the planets? The first is finish'd in a natural day; The second thus: as Saturn in thirty years; Jupiter in twelve; Mars in four; the Sun, Venus, and Mercury in a year; the moon in twenty-eight days. Tush, these are freshmen's suppositions. But tell me, hath every sphere a dominion or intelligentia? Mephistopheles: Ay. Faustus: How many heavens, or spheres, are there? Mephistopheles: Nine: the seven planets, the firmament, and the empyreal heaven. Faustus: Well, resolve me in this question: Why have we not conjunctions, oppositions, aspects, eclipses, all at one time, but in some years we have more, in some less? Mephistopheles: Per inæqualem motum respectu totius*. *On account of their unequal motion in relation to the whole Faustus: Well, I am answered. Tell me who made the world. Mephistopheles: I will not.
|
|
||||||||