

 |

|
|
| |||
|
通过分量计算模和方向的话,我们可以用毕达哥拉斯定理以及tan 函数的定义:
假如我们说“向东2.0米,然后向北1.0米”,这个“东”又是指什么呢?它只是告诉我们方向,那么它有模吗?现在我们给这个“东”指定模,让它为1(不是1米,就只是1)。然后我们就可以把“”向东2.0米”看作是一个乘积了。这里,东就是一个单位向量了。
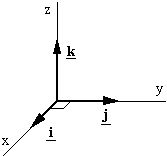 我们分别用 i, j和k 表示x、y和z方向的单位向量。然后我们就可以写出:
我们分别用 i, j和k 表示x、y和z方向的单位向量。然后我们就可以写出:
当然,并不是所有情况下我们都要用到单位向量。我们用“正x方向”代替i。但是,单位向量除了简洁以外,另一个好处就是用它做向量的计算会变得非常简单,在之后向量的加减乘部分我们就会明白这点。
偶尔你也会在圆、圆柱或球形的极坐标中看到单位向量。这些单位向量包括半径r方向、θ、φ和/或z方向。不过在Physclips的力学部分我们不会用到这些单位向量。
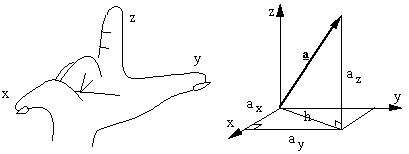 在一个(x,y,z)坐标系中,我们要用到笛卡尔坐标系的三个单位向量,向量 a写作:
在一个(x,y,z)坐标系中,我们要用到笛卡尔坐标系的三个单位向量,向量 a写作:
毕达哥拉斯定理在三维空间同样适用,如图所示。对于向量 a,它的模是? 首先,用毕达哥拉斯定理计算斜边h:
四维的情况呢?比如在(x1,y1,z1,t1)和(x2,y2,z2,t2)处的两个事件的时空距离?这就涉及相对论了,相关的介绍请看这里。简单来说,我们写作a2 = (x22 − x12) + (y22 − y12) + (z22 − z12) − (ct22 − ct12)。 |
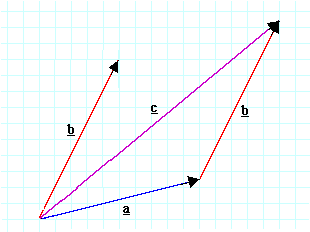
向量加法首先请注意,在这张图中,两个箭头标记为b。但是,这两个箭头的的模和方向相等,所以 他们是相等的向量。现在让我们把图中的 a和 b 看作是位移。就说我沿着位移 a 移动好了(也就是我从 a 的末尾移动到箭头处)。将位移 b加上去,就是从我刚才到达的地方,也就是 a的箭头处,沿着 b继续移动。换句话说,我把两个向量头尾相连。所以,在图中,
可以用几何图形清楚地解释加法。但是,如果我們知道(或者可以找到)向量的分量的話,就很容易写出:
cx i + cy j = (ax + bx )i + (ay + by )j.
cy = ay + by . |
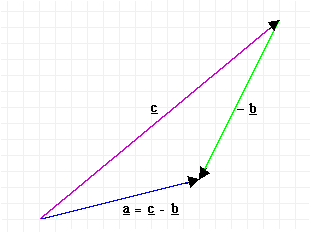
让我们回到之前的实例,
|
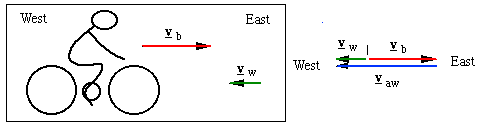
顶风什么感觉?
风相对地面的速度, vw 通常称为真实速度,风相对地面上移动物体的速度称为视速度, vaw。所以这个问题也可以这样表述:视速度是多少?或者说在一个同你一起移动的坐标系中风速 vaw是多少? 答案很简单:风相对你以 vaw 的速度移动,你相对地面以 vb的速度移动,所以真实风速是:
vaw = vw − vb.
所以骑自行车顶风时的风速是15 m.s−1 ——这个答案相信你在心里就已经算出来了。 |
|
侧风什么感觉?
这里用和之前实例中相同的颜色来表示。在这个三角形中,计算顶角:tan−1vw/vb。注意如果vw < vb,通常是这样的,则由于侧风引起的视速度会非常接近顶风时的视速度,正如这个实例。 骑行者经常说“顺风很少,下坡顺风更是不可能发生的。”你能用向量减法来解释这句话吗? 速度的加减对于水手来说也是非常重要的。首先因为船相对水的速度加上水相对地面的速度才是船相对地面的速度。而且,船上测得的风速,是 “真实速度”(也就是风相对地面的速度)减去船相对地面的速度。见 航海物理 中的实例。 也可以看 传送带上的飞机。
|
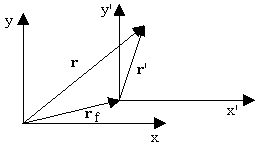
不同体系中的位置,速度和加速度这里让我们讨论更一般的情况:假设一个质点在一个固定在地面上的体系中的位置为r 。如果让这个体系相对地面匀速运动,相对地方面位置为 rf。所以该体系的移动速度是 vf = drf/dt。把这个质点在移动的体系中的位置称为 r',所以
|
i.j = j.k = k.i = 0.
|
|
|
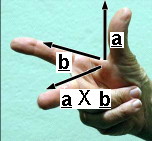
a X b 的方向是在右手系中的垂直于 a 和b的方向。 a X b 读作“a叉 b”。
|
|
这里要指出一个可能令人出乎意料的情况。为了证实之前的记忆方法,现在让你的右手大拇指指向 北,食指指向东。是的, 北 X 东手心确实向 下。现在让你的大拇指指向 东然后食指指向北 。现在你会发现 东 X 北 手心向上。换句话说就是:
|
|i X i| = 1*1 sin 0 = 0. 所以: i X i = j X j = k X k = 0.
a X b = (ax i + ay j + az k) X (bx i + by j + bz k)
+ (axby) i X j + (aybz) j X k + (azbx) k X i + (aybx) j X i + (azby) k X j+ (axbz) i X k, 所以,合并简化后就有:
bx by bz bx i j k i j |
|
||||||||