
 |
|
|
| ||
|
To obtain the magnitude and angle from the components, we can use Pythagoras' theorem and the definition of the tan function, respectively, to give us:
If we say "Go 2.0 metres East, then 1.0 metre North", what does "East" mean? It tells us just direction, so does it have a magnitude? Suppose we give "East" a magnitude of one (not one metre, just one). Now we can treat "2.0 metres East" as a product. In this sense, East is a unit vector.
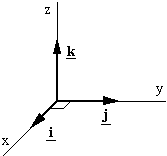 We reserve the vectors i, j and k as unit vectors in the x, y and z directions, respectively. Now we can write:
We reserve the vectors i, j and k as unit vectors in the x, y and z directions, respectively. Now we can write:Of course, we don't need to use unit vectors in all circumstances. We could say "in the positive x direction" instead of i. However, apart from brevity, the advantage of unit vectors is that we can now do vector algebra very simply, as we shall see in the sections on addition, subtraction and multiplication of vectors.
Incidentally, you may also see unit vectors in circular, cylindrical or spherical polar coordinates. These include a unit vector in the radial or r direction and unit vectors in the θ, φ and/or z direction. However, we don't use these in the Mechanics section of Physclips.
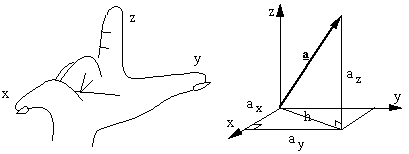 In an (x,y,z) coordinate system, we shall use all three unit vectors of the Cartesian system and write, for a vector a:
In an (x,y,z) coordinate system, we shall use all three unit vectors of the Cartesian system and write, for a vector a:
A useful result comes from an extension of Pythagoras' theorem to three dimensions, which is also shown in that diagram. For the vector a, what is the magnitude a? First, we can use Pythagoras for the hypotenuse h and write:
What about four dimensions? What if we want the spacetime separation of two events at (x1,y1,z1,t1) and (x2,y2,z2,t2)? This takes us to special relativity, which we introduce here. Briefly, we'd write a2 = (x22 − x12) + (y22 − y12) + (z22 − z12) − (ct22 − ct12). |
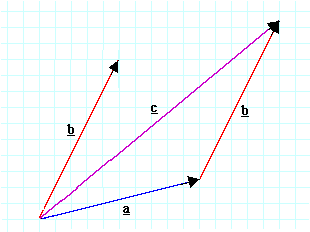
Adding vectorsFirst note that, on this diagram, two arrows are labelled b. However, each arrow has the same magnitude and the same direction, therefore they are the same vector. Now let's think of vectors a and b in this diagram as displacements. Let's say I move through the displacement a (ie, I travel from the tail of a to its head). To add a displacement b to this, I shall move through b, starting from where I have just arrived, at the head of a. In other words, I put the two vectors head to tail. So, in this diagram,
To quantify the addition, one could use geometry. However, if we know the components (or if we can find them) it's often easier to write:
cx i + cy j = (ax + bx )i + (ay + by )j.
cy = ay + by .
|
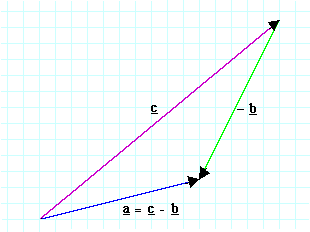
Let's take our previous example and rearrange |
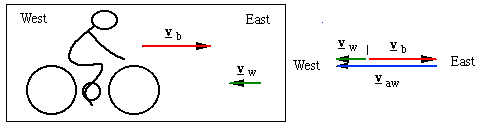
What does a head wind feel like?
The velocity of the wind with respect to the ground, vw is usually called the true wind, and the velocity relative to an observer moving over the ground is called the apparent wind, vaw. So this question would often be expressed thus: what is the apparent wind? Or, alternatively, what is the velocity of the wind, vaw, in a coordinate system moving with you? Here, it's easy: the wind is travelling at vaw with respect to you, and you are travelling at vb with respect to the ground, so the true wind is:
vaw = vw − vb.
so the cyclist has a head wind of 15 m.s−1 – an answer that you probably did in your head already. |
|
What does a cross wind feel like?
The same colour coding is used as in the previous example. Using the right angle triangle, we calculate the angle at the top: it is tan−1vw/vb. Note that, if vw < vb, which is often the case, the apparent wind due to a side wind can be reasonably close to an apparent head wind, as is shown here. Cyclists often say "Tailwinds are rare, and downhill tailwinds don't happen." Using vector subraction, can you explain this belief? Addition and subtraction of velocities is also very important to sailors, first because the velocity of the boat over the water adds to that of the water over the ground to give the boat's velocity with respect to the ground. More importantly, the relative velocity of the wind, as measured on the boat, is the 'true wind' (ie the velocity of the wind with respect to the land) minus the velocity of the boat with respect to the land. See The physics of sailing for examples. Also see Plane on a conveyor belt.
|
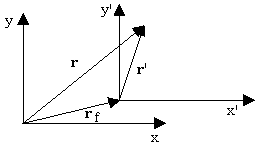
Position, velocity and acceleration in different framesLet's derive that more generally: suppose that we measure position r in a frame of reference fixed on the ground. Let the origin of a frame moving at constant velocity with respect to the ground be rf with respect to the frame fixed on the ground. So the velocity of the moving frame is vf = drf/dt. Let position in the moving frame be r', so
|
i.j = j.k = k.i = 0.
|
|
|
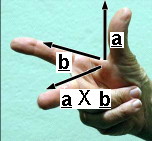
a X b is at right angles to a and b in a right handed sense. a X b is pronounced "a cross b".
|
|
Now for a surprise. To verify the mnemonic above, put your right thumb in the North direction and your forefinger in the East direction. Yes, North X East is indeed Down. Now put your right thumb in the East direction and your forefinger in the North direction. You have now seen that East X North is Up. In other words:
|
|i X i| = 1*1 sin 0 = 0. So: i X i = j X j = k X k = 0.
a X b = (ax i + ay j + az k) X (bx i + by j + bz k)
+ (axby) i X j + (aybz) j X k + (azbx) k X i + (aybx) j X i + (azby) k X j+ (axbz) i X k, so, collecting terms and using the simplifications given above:
bx by bz bx i j k i j and take the diagonals between the elements in the top two rows and multiply them by a term in the third row. But enough algebra! Now it's time to have a look at the Rotation chapter on Physclips, or the section on electric motors and generators, in order to see the examples that required cross products, and to see how they work in the real world. The physics of sailing has some interesting examples of vector addition and subtraction. |
|
||||||||