The electromagnetic spectrum
From Physclips:
Physics with animations and film.
|
| Electromagnetic waves fill a spectrum with wavelengths
from thousands of kilometres long down to wavelengths more than 1020 times
smaller. They may be detected using a range of quite different instruments.
As the
graphic shows, visible light comprises only a tiny fraction of this spectrum: less than an octave. Photon energies also vary over this huge range: in the
radio band we collect huge numbers of photons, each having only a tiny
energy. The phase of the photons in a radio transmission is not random:
it is such that their fields add together, and we can therefore observe
their combined electric and magnetic fields as they oscillate in time
and space. For gamma rays, we may observe the effects of many charged
particles, all created by a single photon.
This page discusses the uses and properties of the different
bands, and several of the important concepts associated with
electromagnetic waves.
Standard names for radio bands
In one classification system, the waves used for radio communication
(and other purposes) are neatly divided up in decades, ie divided
into bands whose wavelengths and frequencies vary over a factor
of 10. In wavelength, the bands begin and end on metres times a
power of ten. Because the speed of light is close to 3 10 8m/s,
when these bands are expressed in frequencies, their limits are
3 times a power of 10 Hz. eg for 3 GHz, λ =
c/f = 10 cm. The names of the bands are:
- Sources in the Super Low and Extra Low Frequency
bands (SLF and ELF) are mainly accidental or
natural. For instance, electricity authorities have very
long antennae, called power lines, that radiate at 50 or
60 Hz. This signal is picked up as 'hum' and is cursed
by electrical engineers everywhere. A large natural source
is the interaction of the solar wind with the ionosphere
that produces low frequency currents (telluric currents)
in the earth and oceans, and these are studied by geophysicists
to deduce, inter alia, the presence of ore bodies whose
electrical conductance differs from that of the surrounding
crust. Like ULF, these bands may be used for communication
with submarines, with low information rates.
- 300 Hz - 3 kHz. Ultra Low Frequency (ULF).
Electromagnetic waves in this range are not strongly absorbed
by water or the earth. They may therefore be used to communicate
with submarines and with mines. One disadvantage is that, with
such low frequency, one can only modulate their amplitude or
frequency very slowly (eg with morse code) so they cannot carry
much information. This is not a disadvantage if only the phase
is required, as is the case for navigation systems. The wavelengths
are so long that antennae may be huge.
- 3 - 30 kHz. Very Low Frequency (VLF).
Again, the information carrying capacity is limited. These
are used in navigation systems.
- 30 - 300 kHz. Low Frequency (LF).
This band has the advantage that it can propagate around the
Earth, by refraction and reflection at the ionisphere or the
surface of the Earth itself. Indeed, these two conductors form
a waveguide for waves in this range, which can therefore be
used to communicate across the oceans and around the world.
- 300 kHz - 3 MHz. Medium Frequency (MF).
(This includes the AM radio band: see below). These waves are
not so well reflected/refracted by the ionosphere, but at night
there is enough reflection that one can pick up radio stations
hundreds or thousands of km away. This is not possible with
the much shorter waves used for FM radio or television: for
these you need an unobstructed path to the transmitter that
is not much different from a straight line.
- 3 - 30 MHz. High Frequency (HF).
This is also known as the Short Wave band. It includes the
CB band (see below) and the channels used for radio control.
As the frequency of the carrier wave increases, it becomes
possible to encode more information and to crowd channels (proportionately)
closer together.
- 30 - 300 MHz. Very High Frequency (VHF).
(includes FM radio and television). Antennae are often made
to be about one quarter or one half wavelength long.
- 300 MHz - 3 GHz. Ultra High Frequency (UHF).
(GHz = 109 Hz). This includes some television and
mobile phones: see below. Many channels are available.
- 3 - 30 GHz. Super High Frequency (SHF).
(roughly corresponds to microwave band) Used for communication
with satellites.
- 30 - 300 GHz. Extra High Frequency (EHF).
Not much used for radio communication (yet), because of the
technological difficulty of encoding and decoding amplitude
and frequency modulation at such high frequencies.
Here ends the radio band. Hereafter, wavelengths are used almost
exclusively, partly for traditional reasons, and partly because
frequencies in the THz range (THz = 1012 Hz) are difficult
to measure directly. (They can be measured by heterodyning: observing
the difference frequencies they make with reference signals.)
Infrared, visible, ultraviolet, X and gamma rays
- Infrared: wavelengths longer
than visible and up to about 1 mm (often measured in microns
or micrometres, symbol μm). Infrared
radiation can be felt as radiant heat: eg when you stand in
front of a fire. Some snakes have IR sensors. The military
uses IR binoculars for the same reason as snakes do: to find
mammals, who are usually warmer than our surroundings.
- Visible: Wavelengths are about
400 nm (violet light) to 700 nm (red light). A nanometre, symbol
nm, is 10-9 m. The sun radiates most strongly in
this range, and our atmosphere does not absorb it (Los Angeles
excepted). This is not a coincidence: we have evolved on this
planet in this atmosphere, so of course we have evolved sensors
that use the available radiation. (Pace Drs Pangloss,
Liebniz and certain other naifs. Any readers interested in
teleology should follow this link.) Visible
light can cause chemical reactions (eg vision and photosynthesis)
but usually does not. The diodes used in solar cells work at
a potential difference of about 0.6 volts, so every visible
photon has enough energy to shift one electron across the interface.
See the introductory
page on the photovoltaic effect.
- Ultraviolet: wavelengths shorter
than visible, down to about 10 nanometres. UV is more useful
in chemistry, because each photon has energy comparable with
that of a chemical reaction. It is dangerous for the same reason:
a UV photon has enough energy to damage DNA molecules in your
cells (so remember to wear sunscreen and a hat). If objects
are hotter than the sun (eg some massive young stars), they
radiate in the UV. Bees can see in the near UV and so flowers
have UV colours to attract them. (Bees can also see the polarisation
of light, which they use to navigate, but that's another story.)
When the energy of photon is high enough, it is often expressed
in electron volts: an ultraviolet photon with 10 eV or more
has enough energy to ionise an atom if its outer electron is
held at an electric potential of 10 Volts. This is typical
of the binding energies of atoms, which is why UV is chemically
potent.
- X rays: wavelengths from several
nm to 10 pm (a picometre is 10-12 m).
Xrays with wavelengths comparable to atom dimensions are used
to determine the structure of crystals, in a technique developed
by the Australian physicists, William
and Lawrence Bragg, for which they received the Nobel prize
in 1915. X rays are divided informally into 'soft' X rays with
long wavelengths and 'hard' X rays with shorter wavelengths
and higher energies. Their energies are enough to ionise atoms
and to destroy chemical bonds. They are produced naturally
by some radioactive sources, or by very hot objects
like neutron stars. They are also produced by smashing high
energy electrons into metal targets: X rays thus produced are
used to treat cancers including breast cancer. Soft X rays
are stopped by (enough) air. Hard X rays can penetrate deeply
into tissue.
- Gamma rays: wavelengths less
than about 10 pm. They have very high energy, and often
come from deep space, sometimes in bursts from cataclysmic
cosmic events, such as the collapse or collision of stars.
A 10 GeV cosmic ray has the same energy as an electron would
have it were accelerated through 10 billion volts. This is
enough energy to cause a chain reaction of ionisation events
in the Earth's atmosphere, leading to a shower of charged particles.
|
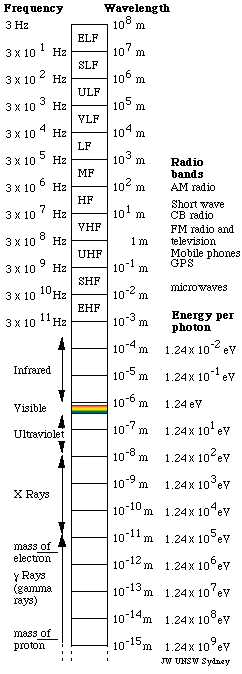
The electromagnetic spectrum
|

Common names for radio bands.
For practical purposes, other divisions of the radio part of the spectrum are
used, including those bands allotted for specific types of communication. So
for instance people talk of the AM radio band, of the CB band etc. Here are
some
examples:
- AM radio: 535 - 1,700 kHz (0.535 - 1.7 MHz)
Have a look at the dial on your radio and check the frequency of your favourite
AM station. Then divide this into the speed of light to get the wavelength.
Fortunately, you do not need an antenna that has a comparable length, although
the strength of the signal will increase as you increase the antenna length.
- Short wave - several different bands in the
range 5.9 - 26.1 MHz
- Citizens band (CB) radio - Several bands
around 27 MHz.
- FM radio: 88 - 108 MHz. If the announcer
says 102.5 FM, she is telling you the frequency of her station. The wavelength
are about 3 metres, so simple antennae should be about 1/4 or 1/2 this
length. To get an idea of how crowded the EM spectrum is, have a look at this scan (click on the yellow graphic) provided
by Balint Seeber, a rather special physics
student at UNSW.
- Television - several different bands between
54 and 220 MHz. (Television carries more information than radio does--pictures
plus sound-- and so needs broader bands for each channel)
- Mobile phones: 824 - 849 MHz
- Global Positioning System: 1.2 -1.6 GHz
- The microwave band is used less formally
for wavelengths of cm down to mm, or frequencies up to 10s or 100s of GHz.
The microwave band is used for radar and long distance trunk telephone
communications. Domestically, it is also used in microwave ovens.
* A FAQ about microwave radiation is whether that produced by
a portable telephone can do damage to the brain to which it may be rather close.
The evidence on this is still not clear. A discussion is at given
in "Microwave Radiation and Leakage of Albumin from Blood to Brain", James C
Lin, IEEE Microwave Magazine, September 2004.
Measurement
Measurement techniques, as well as the uses, vary considerably over the range.
At long wavelengths and low frequencies, we can observe precisely how the electric
and magnetic field vary with time. At the lowest frequencies, we can measure
the time per cycle: at high frequencies, the number of cycles per unit time.
In high GHz or Thz regime, we can no longer measure frequency directly, although
we can calculate it from the wavelength and the speed, or measure it using
indirection means such as heterodyning. Wavelenths are usually measured using
spectrometers, which use the phenomenon of interference. For X rays, the diffraction
gratings in the spectrometers are crystals. For gamma rays, whose wavelengths
are rather smaller than atomic
dimesions, all we can measure is the energy.
Wave vs particle vocabularies for EM radiation
The different limitations involved in measurements have implications for our
choice to use phrases from the wave vocabulary or the particle vocabulary to
describe radiation. For
instance, if we are talking about a transmitted radio wave in the medium
wave band, then huge numbers of photons would combine to make an electric and
a magnetic field whose amplitude we could measure fairly accurately. The intensity
of this wave would be proportional to the square of the amplitude of the electric
field (or the square of the amplitude of the magnetic field). We would not talk
about photons, because it is virtually impossible to measure them individually:
they each have less energy than the kinetic energy of atoms and electrons due
to their thermal motion. We could not distinguish photon capture from the random
thermal motion of electrons in our detector. Even if we cool a detector down
to microKelvin temperature (see graphic) to try to measure photons one at a time,
their energy is so small that it is a difficult task. (Measuring the energy in
radio waves is like measuring water by volume: the molecules of water are there,
but there are very many molecules in every drop so we think of
water as a continuum.)
This radio wave is also different from from ordinary light because it it is
polarised, and because it has a very long coherence length: that is we can
relate the phase predictably over regions of the wave separated by many km.
Further, it is possible to measure and to display the electromagnetic fields
(or rather the voltages they produce in an antenna) as a function of time.
These measurement possibilities dispose us to use the vocabulary of waves to
describe the phenomena.
Light
On the other hand, for light or for waves with shorter waves, we cannot measure
or display E(t): the fields oscillate too fast. Instead, with light, we 'catch
photons': a single photon interacts with a photoreceptor molecule in your eye,
a crystal in a film, an electron in a photocell/photomultiplier tube etc. Because
this is localised in space and time, we are using the particle vocabulary. In
this vocabulary, the intensity of the wave is the energy per photon times the
number of photons per unit area.
Notice that the choice to use wave or particle vocabulary has been made according
to what we can measure (or sometimes what is convenient to discuss). (It is
the opinion of this author that little insight is gained from talking about
wave-particle 'duality' or whether EM radiation 'is' a wave or a collection
of particles. Such talk may, however, help sell popular science books.)
Temperature and colour
2.gif) When photons with a given energy equilibrate
with matter, the thermal energy of the atoms (or electrons, etc) is comparable
with that of the photons. A body in equilibrium with its radiation is
called a black body, and the wavelength at which a black body with (absolute)
temperature T has its greatest radiant power is given by Wien's displacement
law: When photons with a given energy equilibrate
with matter, the thermal energy of the atoms (or electrons, etc) is comparable
with that of the photons. A body in equilibrium with its radiation is
called a black body, and the wavelength at which a black body with (absolute)
temperature T has its greatest radiant power is given by Wien's displacement
law:
λmax = (2.9 x 10-3 m.K)/T.
(See Black body radiation for
more details. There is also a page on thermal radiation and
why clothes work.) Thus the sun, whose surface approximates a black
body with temperature 5,700 K, has maximum radiation at about 500 nm,
in the middle of the visible range. It also emits wavelengths on either
side, and this combination is what we call white light. A hotter star
(or a welding spark) emits proportionately more shorter wavelengths
and so appears blue. A cooler star (or a normal fire) emits mainly
longer wavelengths, and so appears red.
So, if the sun has peak radiation in the green, why doesn't
it look green? The answer has to do with bandwidth (which is
defined as the difference between the frequencies that have half
the power of the maximum, one on either side). The whole visual
bandwidth is less than an octave: from violet to visible red
the wavelength change is less than 100%. The bandwidth of each
of our photo receptor types (formally named L for long, M for
medium and S for shorb, but more commonly known as R, G and B)
is about 20%. The wavelengths of maximum sensitivity for the
three types of photo receptor are 440, 545 an 565 nm, and the
plot shows black body radiancy for these temperatures.
As the plot of black body radiation shows, the bandwidth (frequency
range between points of half maximum power) of a hot body is
rather more than 100%. Looking at this curve, you will see that
a star (or other simple hot body) with maximum radiation in the
green emits very strongly in red, green and blue. In the case
or the sun, or most 5700 K bodies that are close to us, the intensity
is great enough that it will saturate all three colour receptor
types, so that we see white. So how can we see red and blue stars?
The edges of the peaks in the curve are steep. When we see a
blue star, its maximum is in the UV, and red and orange stars
have theirs in the IR. (again, have a look at the curve). One
star with a maximum in the green is the sun. Now you're not supposed
to look at the sun when it is overhead, but I did (very briefly)
and it is white, due to saturation of all photoreceptors. (The
other colours it has near sunrise and sunset are due to atmospheric
scattering or, in the case of the green flash,
due to scattering plus dispersion.)
The background radiation of the universe has a temperature of
a 3 K (or -270°C), and so its spectrum is mainly in the microwave
range. Because we can't see microwaves, it therefore looks 'black'
or invisible to us: it is the radiation coming from the night
sky where there are no stars. This radiation has been travelling
through space ever since the universe was a few hundred thousand
years old, when it first became electromagnetically transparent.
The universe was much hotter then, but because it has expanded
a lot, its radiation has expanded too (wavelengths have become
longer) and become much cooler.
|
Photons and chemistry
Ultraviolet light causes sunburn but visible does not. Why so? Many chemical reactions may be activated by electromagnetic radiation. In the simplest case, one photon interacts with one molecule to initiate the reaction. Each photon has an energy hf, where h is Planck's constant, 6.63 X 10−34 J.s = 4.14 X 10−15 eV.s.
A hydrogen atom has an ionisation energy of about 13 eV so, looking at the spectrum table above, a photon with a wavelength not much shorter than 100 nm (well out in the ultraviolet) has enough energy to ionise a hydrogen atom. Familiar chemical reactions have reaction energies of tens of kJ per mol. Let's take 50 kJ.mol−1 as a reaction energy, divide it by Avagadro's number (6 X 1023 to obtain a value per molecule, and use 1.6 X 10−19 eV per joule to obtain about 0.5 eV per molecule as a reaction energy. So, if it were just a question of getting from initial to final state, a photon in the infrared could supply the energy. Usually, however, there is an actived state with a rather higher energy, so more energy is needed.
Visible light can cause some reactions – such as the photochemistry in our eyes, or on photographic film. Photosynthesis is another (rather complicated) example. Ultraviolet light has more energy available, so UV can cause sunburn, while visible light does not. Hard UV can break carbon-carbon bonds and have serious biochemical effects for people.
Entropy
The (change in) entropy is defined as the heat added reversibly to a system,
divided by its temperature. Usually, heat and radiation go from low entropy (high
T) to high entropy (low T). For example, in a kitchen grill, infrared radiation
at several hundred K (and some weak red light) is transmitted to food at lower
temperature (a few hundred K).
This may seem to raise a paradox: microwaves have
energies of meV, yet in a microwave oven they are used to heat food whose molecules
already have thermal energies of ~0.1 eV. The point here is that the intensity
of the radiation produced by the magnetron or klystron in the microwave oven
is much greater than that of its thermal radiation. Putting your food in interstellar
space, where the microwave radiation is weak, would not cook it: it would simply
cool to about 3 K. Further, the radiation produced by a magnetron (or by a radio
transmitter) is not random, whereas thermal radiation is random. Transmitters
usually produce photons that all have nearly the same phase. For example, a sufficiently
intense but low frequency electric field could produce an electric field of magnitude
100 MV/m, which is enough to ionise atoms, even though one photon might
not have nearly enough energy for ionisation. The field is strong because all
of the photons are in phase and we have a low entropy source. This brings us
to the
relation between entropy and information.
Information
Just like the waves produced by a microwave oven, the radio waves used for communication
consist of huge numbers of photons, all very nearly in phase. This gives them
a much lower entropy than that of a similar number of photons with random phase.
We can then vary the photon phase (usually in the very slight ways associated
with amplitude and frequency modulation) so as to
carry useful information.
Sources whose photons have random phase carry information in other ways. Astronomers
use waves from radio to gamma rays to make images of the sky. To do this, a
minimum of several photons (and usually many more) must be averaged for each
pixel in the image. Under optimal, dark adapted conditions, a single human
photoreceptor must capture several photons in a tenth of a second to be excited
and to give us the sensation of a weak flash of light. Our eyes are at best
about 10% efficient, so this requires us to receive at the cornea several dozen
photons focussed onto one point in the retina. Charged Coupled Detectors are
used in cameras and they are considerably more efficient than our eyes, especially
CCDs operating at very low temperatures.
History
This page is a distillation of the work of many people who have worked to understand
electromagnetism, light and heat. Thinking
about light is an essay by physics teacher Russell Downie on the history
of our understanding of light.
|
